La distribución normal estándar

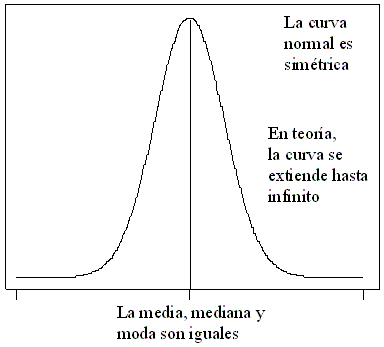
No existe una sola distribución de probabilidad normal, sino una “familia” de ellas.  cada una de las distribuciones puede tener una media (µ) o una desviación estándar distinta (σ).

 Por tanto, el número de distribuciones normales es ilimitado y sería imposible proporcionar una tabla de probabilidades para cada combinación de µ yσ.

 Para resolver este problema, se utiliza un solo “miembro” de la familia de distribuciones normales, aquella cuya media es 0 y desviación estándar 1 que es la que se conoce como distribución estándar normal, de forma que todas las distribuciones normales pueden convertirse a la estándar, restando la media de cada observación y dividiendo por la desviación estándar.

 Primero, convertiremos la distribución real en una distribución normal estándar utilizando un valor llamado Z, o estadístico Z que será la distancia entre un valor seleccionado, designado X, y la media µ, dividida por la desviación estándar σ.

 Como ejemplo de su aplicación supongamos que la media de una distribución normal es 100 libras, y la desviación estándar, 2 libras. Considera que estás interesado en determinar el área entre un valor de 113 libras y la media de 100 libras.

 Primero se convierte la distribución, a lo que se conoce cono estandarización, de una distribución normal estándar, utilizando el llamado valor z o desvío normal z. El valor z es la diferencia (desviación) entre un valor seleccionado, denotado por x y la media poblacional, dividida entre la desviación estándar de la población.

El valor z mide la distancia entre el valor específico x y la media, en unidades de desviación estándar. Así, el valor de z para el ejemplo dado es: z = = 113-/100/2=6.5. unidades de desviación estándar.

Distribución Normal estándar En efecto, todas las distribuciones Normales son lo mismo si usamos las unidades de medida σ alrededor de su media µ que es el centro.

 Definición

 Si x es una observación de una distribución con media µ y desviación estándar σ, el valor estándar de x es z Este valor estándar también se le conoce como valor-z. El valor-z nos indica cuantas desviaciones estándares esta la observación original de si media y en que dirección. Las observaciones mayores que su media toman valores positivos cuando se estandarizan mientras los valores que son menores a su media toman valores negativos.

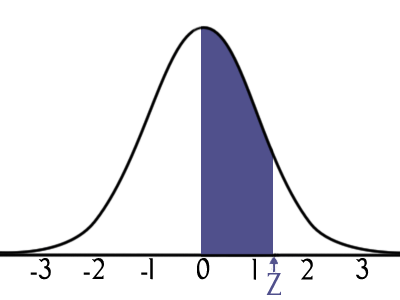
Puedes usar la tabla de abajo para saber el área bajo la curva desde la línea central hasta cualquier línea vertical "a valor Z" hasta 3, en incrementos de 0.1

Esto te dice qué parte de la población está dentro de "Z" desviaciones estándar de la media.

En lugar de una tabla LARGA, hemos puesto los incrementos de 0.1 hacia abajo, y los de 0.01 de lado.

Por ejemplo, para saber el área debajo de la curva entre 0 y 0.45, ve a la fila de 0.4, y sigue de lado hasta 0.45, allí pone 0.1736

Como la curva es simétrica, la tabla vale para ir en las dos direcciones, así que 0.45 negativo también tiene un área de 0.1736

Presentación probabilidad from ojitos55

Area bajo la curva

Áreas bajo la curva normal Para una distribución de probabilidad normal:

1. Aproximadamente 68.27% del área bajo la curva normal está entre μ – σ y μ + σ. Esto puede expresarse como μ ± σ.

2.Aproximadamente 95.45% del área bajo la curva normal está entre μ – 2σ y μ + 2σ. Lo que se expresa μ ± 2σ.

 3.Casi toda el área (99.73%) bajo la curva normal está dentro de tres desviaciones estándares respecto de la media (a uno y otro lado), lo cual se escribe μ ± 3σ.

Estos valores los expresamos de otra forma: el área bajo la curva normal entre µ σ µ σ y − + es aproximadamente 0.6827, el área entre µ σ µ σ y − + 2 2 es aproximadamente 0.9545 y el área entre µ σ µ σ y − + 3 3 es aproximadamente 0.9973. Observa que el área total bajo la curva es: 1.00

Distribución normal

La distribución de probabilidad conocida como distribución normal es  la más importante de las distribuciones estadísticas por la cantidad de fenómenos que explica.

A la distribución normal también se la denomina con el nombre de campana de Gauss, pues al representar su función de probabilidad, ésta tiene forma de campana.

La distribución normal también aparece en muchas áreas de la propia estadística. 

Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.

Definición de distribución de probabilidad normal:

 La Normal es la distribución de probabilidad más importante. Multitud de variables aleatorias continuas siguen una distribución normal o aproximadamente normal. Una de sus características más importantes es que casi cualquier distribución de probabilidad, tanto discreta como continua, se puede aproximar por una normal bajo ciertas condiciones

La distribución de probabilidad normal y la curva normal que la representa, tienen las siguientes características: 

• La curva normal tiene forma de campana y un solo pico en el centro de la distribución. 
De esta manera, la media aritmética, la mediana y la moda de la distribución son iguales y se localizan en el pico. Así, la mitad del área bajo la curva se encuentra a la derecha de este punto central y la otra mitad está a la izquierda de dicho punto.

 • La distribución de probabilidad normal es simétrica alrededor de su media.

 • La curva normal desciende suavemente en ambas direcciones a partir del valor central. 

Es asintótica, lo que quiere decir que la curva se acerca cada vez más al eje X pero jamás llega a tocarlo. Es decir, las “colas” de la curva se extienden de manera indefinida en ambas direcciones.

Introduccion a la materia

La estadística es una ciencia formal y una herramienta que estudia el uso y los análisis provenientes de una muestra representativa de datos, busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional.

Sin embargo, la estadística es más que eso, es decir, es la herramienta fundamental que permite llevar a cabo el proceso relacionado de la estadística con la investigación científica.

Es transversal a una amplia variedad de disciplinas, desde la física hasta las ciencias sociales, desde las ciencias de la salud hasta el control de calidad.

Se usa para la toma de decisiones en áreas de negocios o instituciones gubernamentales.

La estadística matemática es escala previa en el estudio de la estadística desde un punto de vista puramente formal, usando la teoría de la probabilidad y otras ramas de la matemática tales como álgebra lineal y análisis matemático. La estadística matemática trata de la obtención de información a partir de los datos. En la práctica tales datos contienen cierta aleatoriedad o incertidumbre. La estadística trabaja con estos datos usando los métodos de la teoría de la probabilidad.

La estadística matemática se divide en:

• Estadística descriptiva: parte que se encarga de describir los datos, esto es, de realizar un resumen y describir sus propiedades típicas.

• Inferencia estadística: parte que elabora conclusiones a partir de una muestra de los datos, en otras palabras, comprueba el ajuste de los datos a determinadas condiciones y proporciona una medida de la bondad de los mismos en términos probabilistas.

La estadística matemática es la base teórica para muchas prácticas en la estadística aplicada.